Test 4 Review of MTH 3720 Introduction to Differential Equations, Fall 2020

Tuesday, November 24

Test 4 topics include Quizzes {12,13}, and the topics from §4.1, §4.3, §4.4, §4.5, §4.6.
Review for test 4.

$\S 4.1$ Definitions and Examples of Second Order ODEs: $\S 4.1$ introduced second order ODEs and asked through verbal descriptions to set up IVPs for mass-spring systems and series RLC circuits.
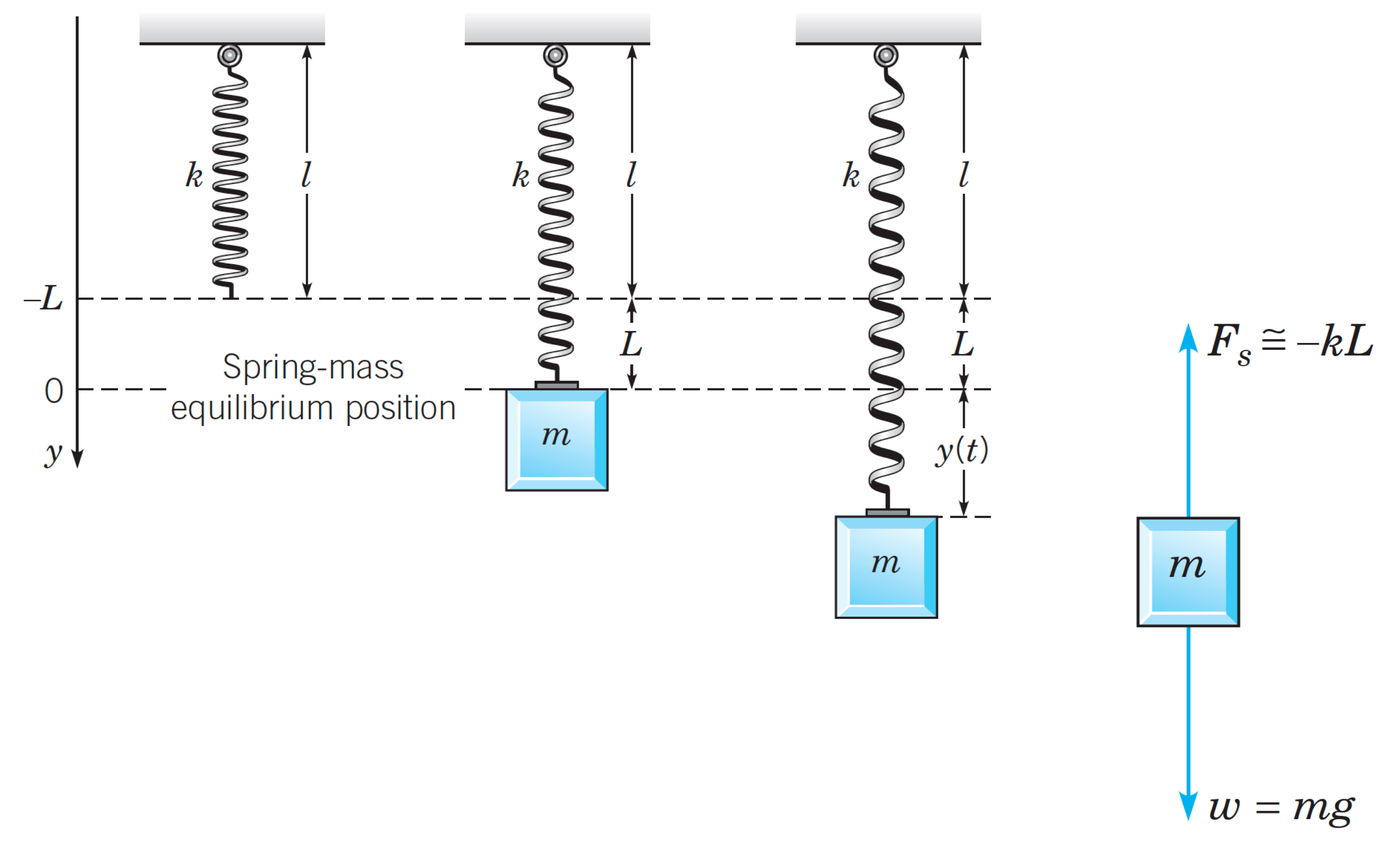
1. At rest $F_s=F_g$, so $kL=mg$, hence $\boxed{k=\frac{mg}{L}}$
2. The weight $w=mg=F_g$, so $\boxed{m=\frac{w}{g}}$
3. At any position $y(t)$, we have $F_s=-k[L+y(t)]$ and $$F_g=w=mg, \text{ and } F_d=-\gamma y'(t)$$
4. There is also external driving force $F_{ex}(t)$
5. Newton's law of motion says $\boxed{my''=\sum \text{Forces}}$ so we end up with \begin{align*} my''(t) &= F_g+F_s+F_d+F_{ex} \\ &= \underbrace{mg-kL}_{\text{cancel out}}-ky(t)-\gamma y'(t)+F_{ex}(t) \\ my''+\gamma y'+ky &= F_{ex}(t) \end{align*}
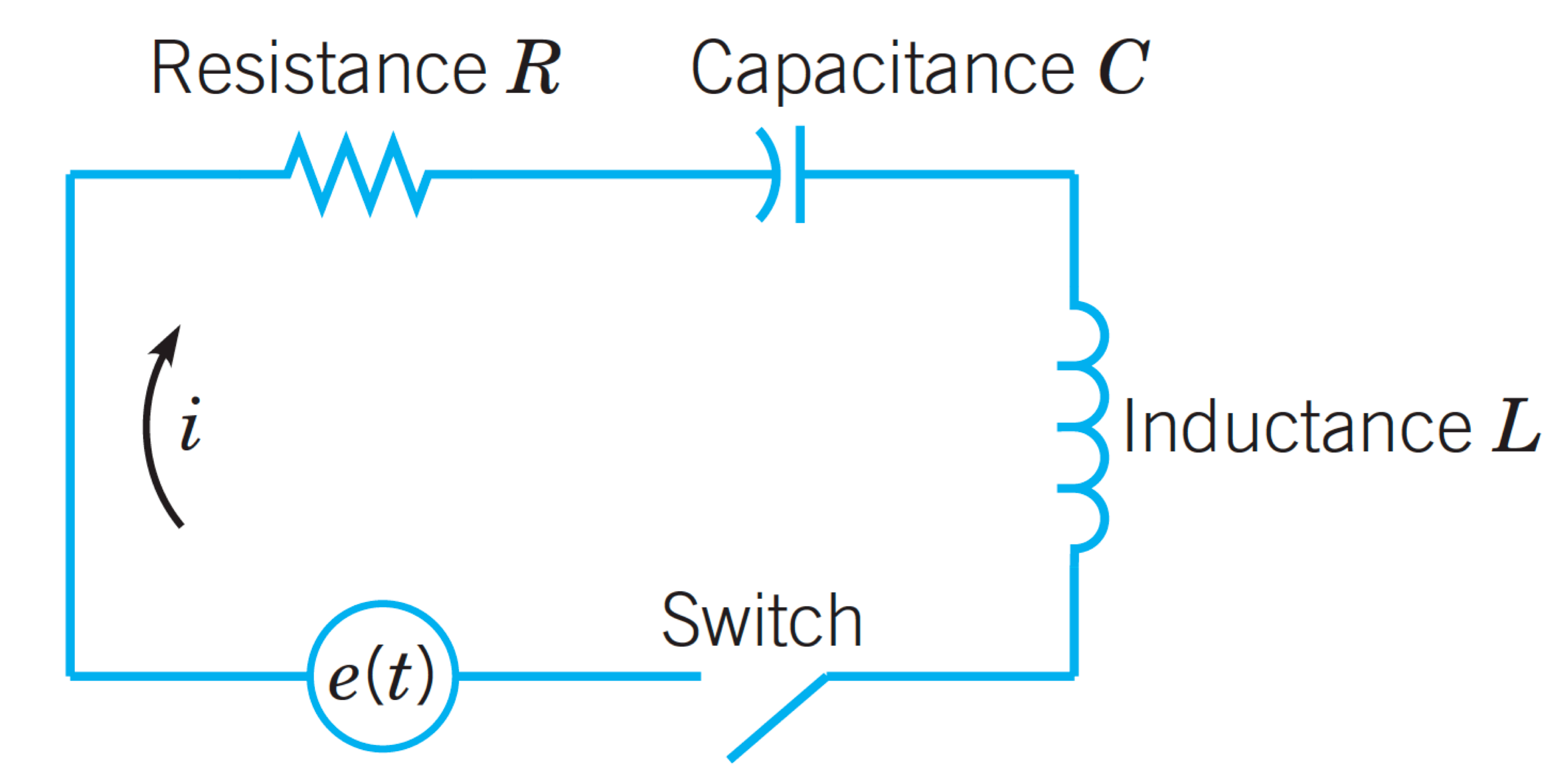
As for the series RLC circuit you need to know the following:
1. Charge is $q(t)$ coulumbs.
2. Current $i(t)=\frac{d q}{dt}$ amperes.
3. $v_R(t)=iR$, $v_C=\frac{q}{C}$ and $v_L=L\frac{di}{dt}$.
4. Kirchhoff's voltage law says: in a closed CKT, voltage across active source equals to the sum of voltages across passive elements. In symbols $$ L\frac{di}{dt}+Ri+\frac{1}{C}q = e(t)$$ uses both $q(t)$ and $i(t)$.
\begin{align*} Lq''+Rq'+\frac{1}{C}q & = e(t), \hspace{3mm} q(t_0)=q_0, \, q'(t_0)=i(t_0)=i_0. \hspace{4mm} \text{in terms of $q$}\\ Li''+Ri'+\frac{1}{C}i & = e'(t), \hspace{3mm} i(t_0)=i_0, \, i'(t_0)=i'_0. \hspace{1.8cm} \text{in terms of $i$} \end{align*} Problems 10, 11, 13, 14 and 15 on page 225 are verbal descriptions asking you to set up an IVP. This is about figuring out the coefficients and ICs in $\boxed{ay''+by'+cy=0, \,\,\, y(0)=y_0, \, y'(0)=y_1}$
$\S 4.2$ Theory of Second Order Linear Homogeneous ODEs: For problems 2 and 6, reduce the IVP to standard form $y''+p(t)y'+q(t)y=g(t)$, then determine the longest open interval $a < t < b$ over which the coefficients $p(t)$ and $q(t)$ are continuous, and finally select the interval $I$ which contains $t_0$. By Theorem 4.2.1 on page 229, the unique solution to the IVP is guaranteed to exist over $I$. The point here is that it might be impossible to find a closed form solution, so before we start running numerical approximations using computer, we are guaranteed by this theorem that at least what we are looking for exists.
For problems 10 and 12, use $\boxed{W[y_1, y_2](t)=\left|\begin{array}{cc}y_1(t) & y_2(t) \\y_1'(t) & y_2'(t)\end{array}\right|}$
Problems 13 and 22 are straight forward verifications.
$\S 4.3$ Linear Homogeneous ODEs with Constant Coefficients: $\boxed{y(t)=e^{\lambda t}}$ solves homogeneous linear ODE of any order, as long as the coefficients are constant. For example:
1. Given $Ay''''+By'''+Cy''+Dy'+Ey=0$
2. Substitute $y=e^{\lambda t}$ to get $A\lambda^4 e^{\lambda t}+B\lambda^3 e^{\lambda t} +C\lambda^2 e^{\lambda t} +D\lambda e^{\lambda t} +Ee^{\lambda t}=0$
3. The polynomial $A\lambda^4 +B\lambda^3 +C\lambda^2 +D\lambda +E=0$ is called characteristic polynomial.
4. If all zeros of this fourth degree polynomial are distinct, then general solution has the form $y(t)=c_1e^{\lambda_1 t}+c_2e^{\lambda_2 t}+c_3e^{\lambda_3 t}+c_4e^{\lambda_4 t}$. If two roots, say $\lambda_3=\lambda_4$ are the same, then we have $y(t)=c_1e^{\lambda_1 t}+c_2e^{\lambda_2 t}+e^{\lambda_3 t}(c_3+c_4t)$, etc,...
Anyhow, $\S4.3$ is about packaging the solution of $\boxed{ay''+by'+cy=0}$ into a matrix-vector form studied in Chapter 3. This was on Quiz 12.
1. Given an IVP $\boxed{ay''+by'+cy=0, \,\, y(t_0)=y_0, \, y'(t_0)=y_1}$. Reflexively write down the corresponding characteristic equation $\boxed{a\lambda^2+b\lambda+c=0}$. And find the roots $\{\lambda_1, \lambda_2\}$.
2. Depending on the roots $\{\lambda_1, \lambda_2\}$ three cases follow:
3. To show that solutions $y_1(t)$ and $y_2(t)$ are fundamental, show that $$ W[y_1, y_2](t)=\left|\begin{array}{cc}y_1(t) & y_2(t) \\y_1'(t) & y_2'(t)\end{array}\right|\neq 0 $$
4. To formulate the ODE as a dynamical system $\mathbf{x}'=\mathbf{Ax}$, first rewrite $ay''+by'+cy=0$ in standard form $y''+\frac{b}{a}y'+\frac{c}{a}y=0$, introduce $x_1=y$, and $x_2=y'$ and package into a matrix form $$ \mathbf{x}'=\mathbf{Ax}=\left(\begin{array}{cc}\phantom{-}0 & \phantom{-}1 \\ -\frac{c}{a} & -\frac{b}{a}\end{array}\right)\mathbf{x} $$
5. To write the general solution $\mathbf{x}(t)=c_1\mathbf{x}_1(t)+c_2\mathbf{x}_2(t)$ for $\mathbf{x}'=\mathbf{Ax}$ DO NOT compute the eigenvalues and eigenvectors of $\mathbf{A}$. You already have
  1. Real and distinct $y_1(t)=e^{\lambda_1 t}$ and $y_2(t)=e^{\lambda_2 t}$.
  2. Complex conjugates $y_1(t)=e^{\mu t}\cos(\mu t)$ and $y_2(t)=e^{\mu t}\sin(\mu t)$
  3. Repeated roots $y_1(t)=e^{\lambda t}$ and $y_2(t)=te^{\lambda t}$.
  Instead, write $$\mathbf{x}(t)=c_1\left(\begin{array}{c} y_1(t) \\ y_1'(t)\end{array}\right)+c_2\left(\begin{array}{c}y_2(t) \\ y_2'(t)\end{array}\right)$$
6. Make sure you can sketch the phase portrait and component plots. For sure on the exam.
7. Problems 4, 8, 12, 13, 23, 28, 34, 36, 43-46 on page 251. Review Quiz 12.
$\S4.4$ Free Mechanical and Electrical Vibrations: Page 263, problems 12(a), 13, 14, 17, 18, 19 and 20 were covered by Quiz 13. These six problems are on the exam. The word "Free" means the system is not driven by external disturbance $F_{ex}(t)$. So we are dealing with $my''+\gamma y'+ky=0, \,\, y(0)=y_0, \, y'(0)=v_0$. The words "homogeneous", "free" and "complementary" are synonymous.
- Undamped Free Vibrations: No friction or dashpot, i.e. $\gamma = 0$, or no resistance $R=0$. So we expect sustained or undamped oscillation, and indeed \begin{align} my''+ky &= 0 \,\,\,\, \text{divide by } m\\ y'' + \omega_0^2y &= 0 \\ \lambda^2 +\omega_0^2 &= 0 \,\,\,\, \text{characteristic polynomial}\\ \lambda_{1,2} &= \pm i\omega_0 \\ y(t) &= A\cos \omega_0t + B\sin \omega_0t \\ y(t) &= \sqrt{A^2+B^2}\, \cos (\omega_0t-\delta)\,\, \text{phase-amplitude form} \end{align} To find the phase $\delta$, draw a picture to locate the quadrant with $ (A,B)$ and use $\tan \delta =\frac{B}{A}$.
  Since $\omega_0^2=\frac{k}{m}$, we have the natural frequency of the vibration, $\omega_0=\sqrt{\frac{k}{m}}$.
  Consequently, the period of the motion is $T=\frac{2\pi}{\omega_0}=2\pi\sqrt{\frac{m}{k}}$.
- Damped Free Vibrations: Damping constant $\gamma>0$ or $R>0$ causes exponential damping. \begin{align} my''+\gamma y'+ky &= 0 \\ m\lambda^2 +\gamma \lambda + k &=0 \,\, \text{ characteristic polynomial}\\ \lambda_{1,2} &= \frac{-\gamma \pm \sqrt{\gamma^2-4mk}}{2m} \end{align} The discriminant $\boxed{\gamma^2 -4mk}$ dictates the roots $\{\lambda_1, \lambda_2\}$. This is a repeat of item (b) from above.
  1. Underdamped Harmonic Motion: $\boxed{\gamma^2 -4mk<0}$ so the roots are complex conjugates $\lambda_{1,2}=-\frac{\gamma}{2m}\pm i\frac{\sqrt{4mk-\gamma^2}}{2m}$ or $\lambda_{1,2}=\mu\pm i\nu$ to keep it short. General solution has the form $$ y(t)=e^{-\frac{\gamma}{2m}t}\left( A\cos \nu t + B\sin \nu t \right) $$ This damped motion is no longer periodic, but at least the mass passes through the equilibrium position periodically, so the best we can do is to call $\nu$ a quasi-frequency.
    Analogously we call $T_d=\frac{2\pi}{v}$ the quasi-period.
  2. Critically damped Harmonic Motion: $\boxed{\gamma^2 -4mk=0}$ repeated roots $\lambda_1=\lambda_2$. This is the "sweet spot" between too much damping and too little damping. General solution is $$ y(t)=(A+Bt)e^{-\frac{\gamma}{2m}t} $$
  3. Overdamped Harmonic Motion: $\boxed{\gamma^2 -4mk>0}$ so the roots are real, distinct and negative $$ y(t)=Ae^{\lambda_1 t}+Be^{\lambda_2 t} $$
$\S4.5$ Nonhomogeneous Equations; Method of Undetermined Coefficients: Page 273 problems 2, 3, 4 and 6 are warm up. Problems 9, 10, 13, 14, 17 and 18 are on the exam, and were on Quiz 13. The idea goes as follows, so far we have been studying the solutions that disappear in $L[\phantom{*}]$ $$ \text{input } y(t)? \longrightarrow \boxed{ L[\phantom{*}] = \frac{d^2}{dt^2}\left( \right) +p(t)\frac{d}{dt}\left( \right)+q(t)\left( \right) } \longrightarrow 0 \text{ output}$$ If the coefficients $p(t)$ and $q(t)$ are constant then life is easy and we write $y(t)=c_1y_1(t)+c_2y_2(t)$. $$ \underbrace{y(t)=c_1y_1(t)+c_2y_2(t)}_{\text{input}} \longrightarrow \boxed{ L[\phantom{*}] = a\frac{d^2}{dt^2}\left( \right) +b\frac{d}{dt}\left( \right)+c\left( \right) } \longrightarrow 0 \text{ output} $$ Nonhomogeneous means the system is driven or disturbed by external force, so the picture is $$ \underbrace{y(t)=\overbrace{c_1y_1(t)+c_2y_2(t)}^{\text{disappears inside $L[\phantom{*}]$ }}+Y(t)}_{\text{input}} \longrightarrow \boxed{ L[\phantom{*}] = a\frac{d^2}{dt^2}\left( \right) +b\frac{d}{dt}\left( \right)+c\left( \right) } \longrightarrow F_{ex}(t) \text{ output} $$ If $F_{ex}(t)$ is either a polynomial, exponential, sinusoid or a combination, then we may assume that $Y(t)$ has the same form up to a constant multiples. These "constant multiples" are the undetermined coefficients. The most important case in $\S4.5$ is discussed in Example 5 on page 270 and 271. The comment that follows is crucial:
If the assumed form of the particular solution $Y(t)$ duplicates a solution of the corresponding homogeneous equation, then modify the assumed particular solution by multiplying it by $t$. Always find $y_c(t)=c_1y_1(t)+c_2y_2(t)$ first, if $F_{ex}(t)$ is a duplicate of $y_c(t)$ then modify assumed $Y(t)$ by multiplying by $t$. And don't forget that the general solution to nonhomogeneous linear ODE with constant coefficients has the form $$ y(t)=\underbrace{c_1y_1(t)+c_2y_2(t)}_{y_c(t) \text{ complementary}}+\underbrace{Y(t)}_{\text{particular}} $$ Caution: In practical situations, we use terms "input-output" in reverse. $$ \text{known input } F_{ex}(t) \longrightarrow \boxed{\text{ mechanical system or CKT}} \longrightarrow y(t) \text{ output or response} $$
$\S4.6 $ Forced Vibrations, Frequency Response, and Resonance: Pages 283 and 284, problems 5, 6, 10, 11, 12 and 13.
First topic was Forced Vibrations with Damping $$ \text{known input } F_{ex}(t) \text{ and ICs} \longrightarrow \boxed{\text{ mechanical system or CKT}} \longrightarrow \overbrace{\underbrace{c_1y_1(t)+c_2y_2(t)}_{\text{transient response}}}^{\text{exponential decay} }+\underbrace{\overbrace{Y(t)}^{\text{steady-state}}}_{\text{forced response}} $$ For convenience we divide $my''+\gamma y'+ky=F_{ex}(t)$ by $m$ to get $\boxed{y''+2\delta y'+\omega_0^2y=f_{ex}(t)}$
The system is driven by a generic sinusoid $\boxed{f_{ex}(t)=Ae^{i\omega t}}$ and we study the amplitude and the phase of the response $\boxed{Y(t)=Ce^{i\omega t}}$ and its dependence on $\omega$. Here $C$ is the undetermined coefficient. Next, substitute $Y=Ce^{i\omega t}$ into the ODE and solve for the undetermined coefficient $C$. \begin{align} C(-\omega^2 e^{i\omega t}+2i\delta \omega e^{i\omega t} +\omega_0^2 e^{i\omega t}) &= A e^{i\omega t} \\ C &= A\cdot \frac{1}{\omega_0^2-\omega^2 +2i\delta\omega} \\ G(i\omega) &= \frac{1}{\omega_0^2-\omega^2 +2i\delta\omega} \,\,\,\text{ depends on the system and $\omega$, not on $A$} \\ G(i\omega) &= \frac{(\omega_0^2-\omega^2)-2i\delta \omega}{(\omega_0^2-\omega^2)^2+4\delta^2 \omega^2}\,\,\text{Gain aka frequency response function} \end{align} The Frequency Response Function $G(i\omega)$ is a complex valued function with real and imaginary parts. In the same way as we can represent $z=a+bi$ in polar form $z=|z|e^{-i\phi}$ where $|z|=\sqrt{z\overline{z}}$ and $\phi =\cos^{-1}\left(\frac{a}{|z|}\right)$, we represent $G(i\omega)$ in polar form as \begin{align} G(i\omega) &= |G(i\omega)|e^{-i\phi(\omega)}=\underbrace{|G(i\omega)|\cos\phi(\omega)}_{\text{real}}-i\underbrace{|G(i\omega)|\sin\phi(\omega)}_{\text{imaginary}} \\ |G(i\omega)| &= \sqrt{G(i\omega)\overline{G(i\omega)}}=\sqrt{\frac{1}{(\omega_0^2-\omega^2) +2i\delta\omega}\cdot \frac{1}{(\omega_0^2-\omega^2) -2i\delta\omega}}=\frac{1}{\sqrt{(\omega_0^2-\omega^2)^2+4\delta^2\omega^2}} \\ \phi(\omega) &=\cos^{-1}\left(\frac{\text{real part}}{\text{hypotenuse}}\right) =\cos^{-1}\left(\frac{\frac{\omega_0^2-\omega^2}{(\omega_0^2-\omega^2)^2+4\delta^2 \omega^2}}{\frac{1}{\sqrt{(\omega_0^2-\omega^2)^2+4\delta^2\omega^2}}}\right)=\cos^{-1}\left( \frac{\omega_0^2-\omega^2}{\sqrt{(\omega_0^2-\omega^2)^2+4\delta^2 \omega^2}} \right) \\ Y(t) &= G(i\omega) Ae^{i\omega t} = \underbrace{\overbrace{|G(i\omega)|}^{\text{gain}}e^{-i\phi(\omega)}}_{G(i\omega)}Ae^{i\omega t} = A|G(i\omega)|e^{i(\omega t -\overbrace{\phi(\omega)}^{\text{phase}})} \\ &= \underbrace{A|G(i\omega)|\cos(\omega t-\phi(\omega))}_{\text{real part}}+i \underbrace{A|G(i\omega)|\sin(\omega t-\phi(\omega))}_{\text{imaginary part}} \end{align} In the case of the real input $f_{ex}(t)=A\cos \omega t$, take the real part of $Y(t)$, that is $\Re\{Y(t)\}$.
- First BIG question: At what frequency does the gain peak? Or in other words: What is the resonance frequency $\omega_{\text{max}}$?
  Easy, set $\frac{\partial |G(i\omega)|}{\partial \omega}=0$, this is problem 13 \begin{align} \frac{\partial |G(i\omega)|}{\partial \omega} &= \frac{\partial ((\omega_0^2-\omega^2)^2+4\delta^2\omega^2)^{-\frac{1}{2}}}{\partial \omega} \\ &= \underbrace{-\frac{1}{2}((\omega_0^2-\omega^2)^2+4\delta^2\omega^2)^{-\frac{3}{2}}}_{\text{irrelevant}}\cdot \underbrace{\left(2(\omega_0^2-\omega^2)(-2\omega)+8\delta^2\omega\right)}_{\text{set to zero}}=0 \\ \omega^2_{\text{max}} &= \omega_0^2-2\delta^2 =\omega_0^2-\frac{\gamma^2}{2m^2}=\omega_0^2\left(1-\frac{\gamma^2}{2mk}\right) \hspace{3mm} \text{Awesome!, this says } \boxed{\omega_{\text{max}}<\omega_0} \end{align}
- Second BIG question: What is the maximum gain? Or in other words: What is $|G(i\omega_{\text{max}})|$?
  Easy, substitute. $$ |G(i\omega_{\text{max}})| = \frac{1}{\sqrt{(\omega_0^2-\omega^2)^2+4\delta^2\omega^2}}\Bigr|_{\omega=\omega_{\text{max}}}=\frac{m}{\gamma \omega_0\sqrt{1-\left( \frac{\gamma^2}{4mk} \right)}} $$
  1. For small $\gamma$ we have a HUGE gain $|G(i\omega)|\cong \frac{m}{\gamma \omega_0}$, really loud resonance.
  2. If $\frac{\gamma^2}{mk}>2$ then $\omega_{\text{max}}$ is imaginary, $|G(i\omega)|$ is monotone decreasing and attains maximum at $\omega =0$. We can't call this resonance.
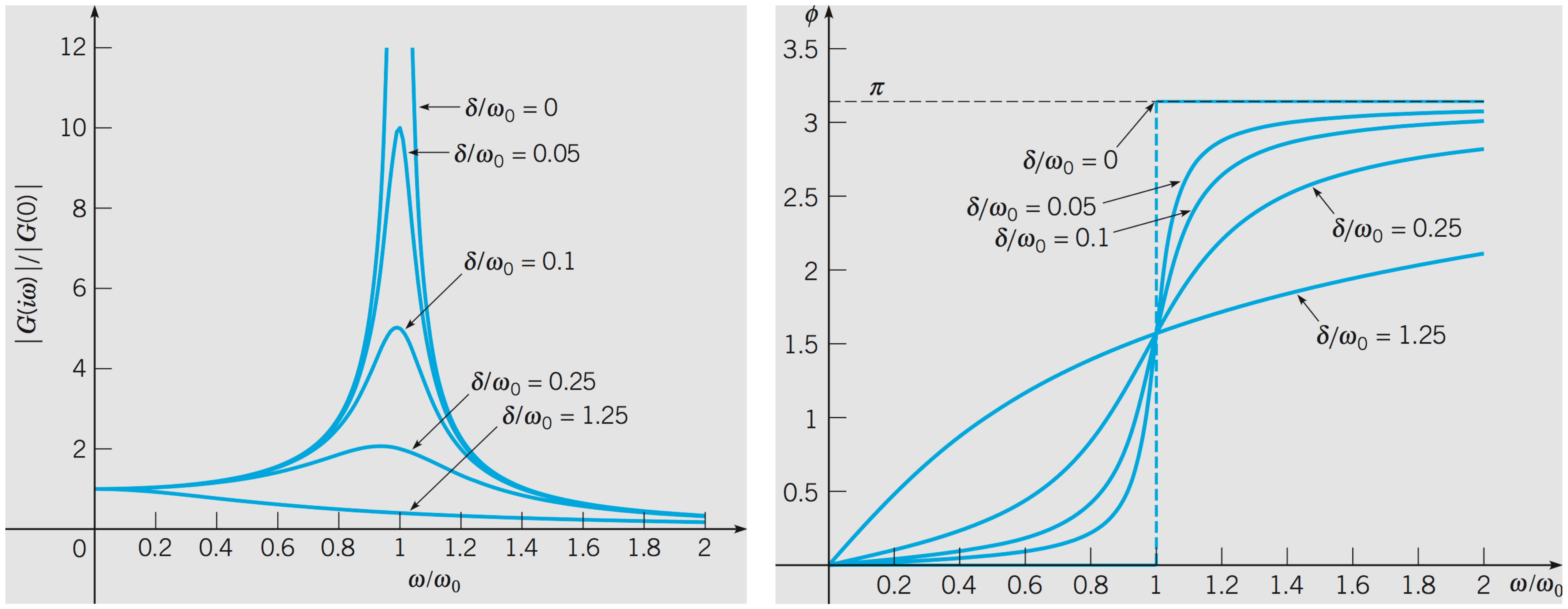
The graph on the left shows a normalized gain $\frac{|G(i\omega)|}{|G(0)|}=\omega_0^2|G(i\omega)|$ versus normalized frequency $\omega/\omega_0$ for several values of $\delta=\gamma/2m$. Note how the peaks in the curves sharpen near $\omega/\omega_0=1$ as $\delta$ gets smaller. It follows from $|G(i\omega)|=\frac{1}{\sqrt{(\omega_0^2-\omega^2)^2+4\delta^2\omega^2}}$ that $$ \lim_{\gamma\rightarrow 0}\, |G(i\omega)| = \frac{1}{|\omega_0^2-\omega^2|}\,\,\,\,\, \text{ and }\,\,\,\,\, \lim_{\gamma\rightarrow 0}\, \frac{|G(i\omega)|}{|G(0)|} = \left|\frac{\omega_0^2}{\omega_0^2-\omega^2}\right| $$ Conversely, as the damping $\gamma$ in the system increases, the peak response diminishes. The graph on the right, illustrates the dependence of the phase angle $\phi$ on the frequency $\omega$.
- For $\omega$ near zero $\phi(\omega)=\cos^{-1}\left( \frac{\omega_0^2-\omega^2}{\sqrt{(\omega_0^2-\omega^2)^2+4\delta^2 \omega^2}} \right)$, says that $\phi \cong 0$, i.e. the response is nearly in phase with the excitation, that is they rise and fall together.
- For $\omega=\omega_0$, $\cos\phi=0$, so $\phi =\frac{\pi}{2}$. The response lags behind the excitation by by $\frac{\pi}{2}$.
- For very large $\omega$, $\cos \phi \cong -1$, that is $\phi\cong \pi$. Nearly out of phase, i.e. the response is minimum when the excitation is maximum, and vice versa.
- Finally note the dependence of the phase transition on $\frac{\delta}{\omega_0}=\frac{\gamma}{2\sqrt{mk}}$. Phase transition occurs abruptly in systems with small damping $\gamma$.
Forced Vibrations without Damping: set $\gamma=0$, hence $\delta =\frac{\gamma}{2m}=0$ to obtain $\boxed{y''+\omega_0^2y=A\cos \omega t}$
- If $\omega\neq \omega_0$ as was covered in the assigned problem 9 of $\S4.5$ page 273, the general solution is $$ y(t)=\underbrace{c_1\cos \omega_0 t + c_2 \sin\omega_0 t}_{\text{due to initial conditions}}+\frac{A}{\omega_0^2-\omega^2}\cos \omega t $$ If the mass is initially at rest $y(0)=0$ and $y'(0)=0$, then $c_1=-\frac{A}{\omega_0^2-\omega^2}$ and $c_2=0$, and $$ y(t)=\frac{A}{\omega_0^2-\omega^2}(\cos \omega t -\cos \omega_0t) $$ Now apply $\boxed{\cos \alpha -\cos \beta = 2\sin\left(\frac{\alpha+\beta}{2} \right)\sin\left(\frac{\alpha-\beta}{2} \right)}$ to get $$ y(t)=\left[ \frac{2A}{\omega_0^2-\omega^2}\sin\frac{(\omega_0-\omega)t}{2} \right]\sin\frac{(\omega_0+\omega)t}{2} $$ The slowly varying factor $\sin\frac{(\omega_0-\omega)t}{2}$ modulates the amplitude of the rapidly varying factor $\sin\frac{(\omega_0+\omega)t}{2}$, and we hear a beat.
- If $\omega = \omega_0$ as was covered in the assigned problem 10 of $\S4.5$ page 273, the general solution is $$ y(t)=c_1\cos \omega_0t+c_2\sin \omega_0t +\frac{A}{2\omega_0}{\color{red}t}\sin \omega_0t $$ The term $t\sin \omega_0t$ becomes unbounded as $t\rightarrow \infty$ and the mass will oscillate violently. In practice, the system will break down or nonlinear effects will prevent unbounded response.
- Notice that the nonhomogeneous (particular) term $\boxed{y(t)=\frac{A}{2\omega_0}{\color{red}t}\sin \omega_0 t}$ in the case $\boxed{\omega=\omega_0}$ can be obtained by taking the limit $\omega\rightarrow \omega_0$ carefully using L'Hôpital's rule \begin{align} \lim_{\omega\rightarrow \omega_0} \left[ \frac{2A}{\omega_0^2-\omega^2}\sin\frac{(\omega_0-\omega)t}{2} \right]\sin\frac{(\omega_0+\omega)t}{2} &= \lim_{\omega\rightarrow \omega_0} \left[ \frac{2A}{(\omega_0+\omega)(\omega_0-\omega)}\sin\frac{(\omega_0-\omega)t}{2} \right]\sin\omega_0 t \\ &= \lim_{\omega\rightarrow \omega_0} {\color{red}t} \cdot \frac{\sin\frac{(\omega_0-\omega)t}{2}}{\frac{(\omega_0-\omega)t}{2}} \cdot \frac{A}{\omega_0+\omega} \sin \omega_0 t \\ &= \left(\lim_{\omega\rightarrow \omega_0} \frac{\sin\frac{(\omega_0-\omega)t}{2}}{\frac{(\omega_0-\omega)t}{2}}\right) \frac{A}{2\omega_0}{\color{red}t} \sin \omega_0 t \\ &= \left( \lim_{\theta \rightarrow 0} \frac{\sin \theta}{\theta}\right) \frac{A}{2\omega_0}{\color{red}t} \sin \omega_0 t \\ &= \frac{A}{2\omega_0}{\color{red}t} \sin \omega_0 t \end{align}

[1] "Differential Equations: An Introduction to Modern Methods and Applications, 3rd edition.", page 268, by James R. Brannan and William E. Boyce.

Test 4 material MTH 3720